فورسفیلد؛ قانونگذار نامرئی دنیای اتمها
در بخش نخست این مجموعه، دیدیم که چگونه شبیهسازی دینامیک مولکولی (MD) با حل عددی معادلات حرکت نیوتن، یک "جهان میکروسکوپی مجازی" میسازد و به ما اجازه میدهد تا حرکات پیچیدهی اتمها و مولکولها را در طول زمان دنبال کنیم. ما از مونتکارلو گفتیم و از این که MD چگونه پلی بین ساختار اتمی و خواص ماکروسکوپی میزند.
اما یک پرسش بنیادین، همچون موتوری پنهان در پس این صحنهی پویا، بیپاسخ مانده است: آن نیروی محرکه، یعنی "F" در معادله ی اساسی F=ma، دقیقاً از کجا میآید؟ چگونه میتوانیم نیروی وارد بر تکتک اتمها در یک سیستم متشکل از هزاران یا میلیونها ذره را محاسبه کنیم؟
پاسخ این پرسش اساسی، در مفهومی کلیدی و جذاب به نام «مدل پتانسیل» یا «فورسفیلد» (Force Field) نهفته است. فورسفیلد را میتوان "قانون اساسی" یا "نقشه راه" دنیای شبیهسازی دانست؛ مجموعهای از قواعد و معادلات ریاضی که به دقت رفتار، برهمکنش و نیروی بین هر اتم را نسبت به اتمهای پیرامونش تعریف و کمّی میکند. بدون یک فورسفیلد دقیق، شبیهسازی ما تنها مجموعهای از ذرات بیارتباط در فضای خالی خواهد بود.
مدلهای مبتنی بر مکانیک مولکولی (MM): فلسفه یک سادهسازی
برای درک شکوه و عظمت یک فورسفیلد، باید به یک تضاد اساسی در دنیای محاسبات بپردازیم: تضاد بین دقت و کارایی. اگر بخواهیم با دقت مکانیک کوانتومی (QM) و با حل معادله شرودینگر، برهمکنش تمام الکترونها را محاسبه کنیم، محاسبات آنقدر سنگین میشود که شبیهسازی حتی یک پروتئین کوچک برای چند نانوثانیه، با قدرتمندترین ابررایانههای امروزی نیز غیرممکن خواهد بود.
اینجاست که زیبایی و نبوغ مدلهای مکانیک مولکولی (Molecular Mechanics) آشکار میشود. این مدلها با یک سادهسازی هوشمندانه، این مشکل را حل میکنند. فلسفه آن را میتوان در دو اصل خلاصه کرد:
۱. نادیده گرفتن الکترونها: در این مدلها، الکترونها به طور صریح محاسبه نمیشوند. در عوض، اثرات کوانتومی آنها در قالب پارامترهای از پیش تعریفشده گنجانده میشود.
۲. مدلسازی مکانیکی اتمها و پیوندها: اتمها به صورت کرههایی با یک شعاع و بار الکتریکی مشخص در نظر گرفته میشوند. پیوندهای شیمیایی بین آنها نیز مانند فنرهایی ایدهآل مدل میشوند که میتوانند کشیده یا فشرده شوند.
این نگاه مکانیکی به جهان اتمی، ما را به معادلهای کلیدی میرساند که هستهی هر فورسفیلد MM را تشکیل میدهد:
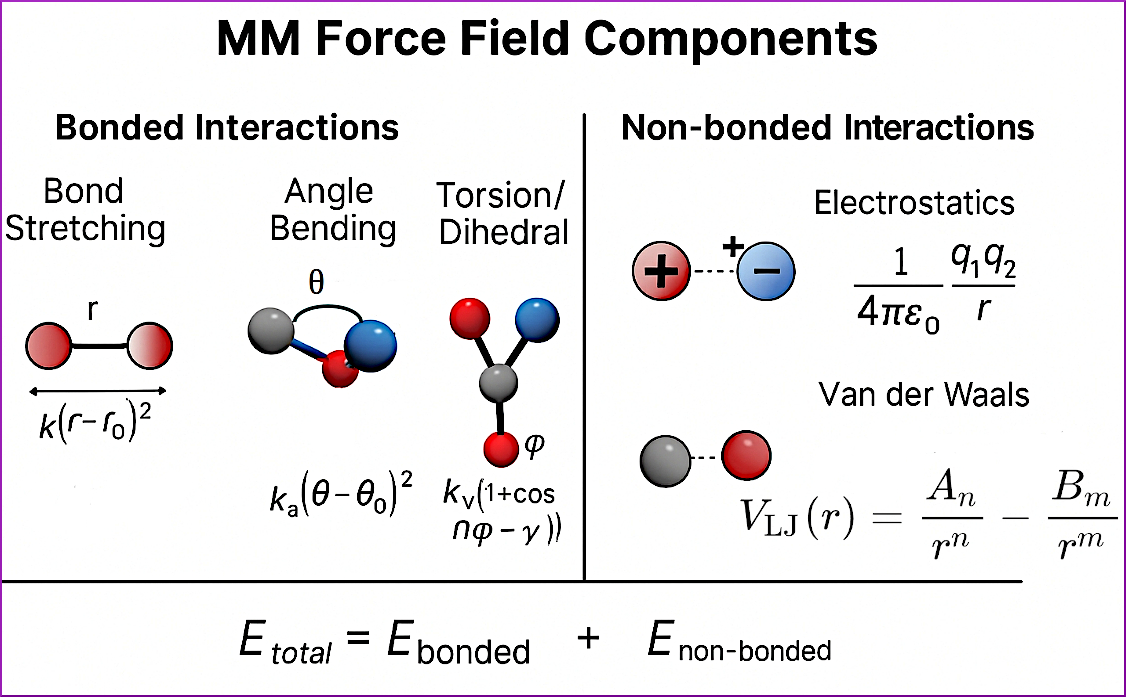
پیوندیE + غیرپیوندیE = E
این معادله میگوید انرژی کل سیستم، حاصل جمع انرژی برهمکنشهای اتمهای پیوندی و اتمهای غیرپیوندی است. اجازه دهید هر یک از این اجزا را با جزئیات بیشتری کالبدشکافی کنیم.
۱. برهمکنشهای پیوندی (Bonded Interactions): ستون فقرات مولکول
این برهمکنشها، اتمهایی را که مستقیماً به هم پیوند شیمیایی دارند، به یکدیگر متصل میکنند و ساختار کلی مولکول را حفظ میکنند. این بخش خود شامل سه جزء اصلی است:
کشش پیوند (Bond Stretching): این مدل، یک پیوند شیمیایی (مثل C-H) را دقیقاً شبیه یک فنر ایدهآل در نظر میگیرد که از قانون هوک پیروی میکند. انرژی مورد نیاز برای کشیدن یا فشردن این پیوند از طول تعادلی آن، با یک ثابت فنر (k) خاص آن پیوند محاسبه میشود. هر چه ثابت فنر بزرگتر باشد، پیوند سفتتر و تغییر طول آن سختتر است.
خمش زاویه (Angle Bending): مولکولها تنها از پیوندهای مستقیم تشکیل نشدهاند. این مدل، انرژی مورد نیاز برای تغییر زاویهی بین سه اتم متصل به هم (مثلاً زاویه H-C-H) را محاسبه میکند. این زاویه نیز یک مقدار تعادلی دارد و انحراف از آن، مانند خم کردن یک فنر، انرژیبر است.
پیچش دووجهی (Torsion/Dihedral): این احتمالاً مهمترین جزء در تعیین شکل سهبعدی مولکول است. انرژی پیچش، به چرخش حول یک پیوند مرکزی (مثلاً پیوند بین دو اتم کربن در مولکول اتان) مربوط میشود. این انرژی است که مانع از چرخش کاملاً آزاد گروههای اتمی میشود و "حالتهای ترجیحی" مولکول را تعیین میکند. برای مثال، همین برهمکنش است که مارپیچ آلفا در پروتئینها را پایدار نگه میدارد.
۲. برهمکنشهای غیرپیوندی (Non-bonded Interactions): هنرنمایی در فواصل دور
این برهمکنشها، که بین همهٔ اتمهای سیستم—حتی آنهایی که مستقیماً به هم پیوند ندارند—اعمال میشوند، برای توصیف واقعبینانهی رفتار مولکولها در کنار یکدیگر مطلقاً حیاتی هستند. اینجاست که شیمی واقعی رخ میدهد!
الکترواستاتیک (Electrostatics): این نیرو، ناشی از برهمکنش بارهای مثبت و منفی اتمهاست و طبق قانون معروف کولن محاسبه میشود. این نیرو برد بلندی دارد و میتواند در فواصل نسبتاً زیاد عمل کند. برای مثال، همین نیرو است که بین گروههای باردار مثبت و منفی در یک پروتئین و یک لیگاند، جاذبه ایجاد میکند. محاسبهی این برهمکنش برای سیستمهای بزرگ، یکی از پرهزینهترین بخشهای شبیهسازی است و اغلب از الگوریتمهای ویژهای مانند «جمع Ewald» برای محاسبهی کارآمد آن استفاده میشود.
واندروالس (van der Waals): این برهمکنش ضعیفتر اما فراگیر، از دو بخش تشکیل شده است:
دافعه (Repulsion): در فاصله بسیار کم، ابرهای الکترونی دو اتم با هم برخورد میکنند و یک دافعه قوی ایجاد میشود (اصل طرد پائولی).
جاذبه (Dispersion/London): در فاصله کمی دورتر، نوسانات لحظهای در توزیع الکترونها، یک دو قطبی موقت ایجاد میکند که دو قطبیهای القایی در اتمهای مجاور به وجود آورده و منجر به یک جاذبه ضعیف میشود.
این دو اثر متضاد، با زیبایی تمام در معادلهی معروف «پتانسیل لنارد-جونز» ادغام میشوند. این پتانسیل یک "چاه پتانسیل" کمعمق ایجاد میکند که فاصله تعادلی بهینه بین دو اتم را مشخص میسازد.
مزیت بزرگ و غیرقابل انکار مدلهای MM، سرعت محاسباتی فوقالعادهی آنها در مقایسه با روشهای کوانتومی است. این سرعت، امکان شبیهسازی سیستمهای بسیار بزرگ و پیچیده—مانند یک پروتئین غوطهور در یک جعبهی پر از مولکول آب با دهها یا حتی صدها هزار اتم—را در بازههای زمانی بااهمیت بیولوژیکی (نانوثانیه تا میکروثانیه) فراهم میکند.
فورسفیلدهای رایج:
یک فورسفیلد خاص، در واقع یک "کیت ابزار" یا یک "کتابچهی قوانین" کاملاً آماده و پارامتریزه شده است. این پارامترها، مانند ثابت فنر یک پیوند C-C، یا شعاع و عمق چاه پتانسیل برای یک اتم اکسیژن،نه به صورت تصادفی، بلکه با دقت بالا از دادههای تجربی (مانند طیفسنجی، بلورشناسی پرتو ایکس) یا محاسبات بسیار دقیق مکانیک کوانتومی استخراج میشوند.
هر فورسفیلد با فلسفهی طراحی خاص خود، برای یک حوزهی کاربردی خاص بهینهسازی شده است. در ادامه، با بزرگان این عرصه بیشتر آشنا میشویم:
AMBER (Assisted Model Building with Energy Refinement): اگر در حوزهی زیستشناسی محاسباتی کار کنید، به احتمال زیاد با این فورسفیلد سروکار خواهید داشت. AMBER به طور تخصصی برای بیومولکولها (پروتئینها، DNA، RNA، کربوهیدراتها) توسعه یافته است. پارامترهای آن برای شبیهسازی این مولکولها در محیط آبی (که محیط طبیعی آنهاست) با دقت بسیار بالا تنظیم شدهاند. از AMBER به طور گسترده در مطالعات تاشدگی پروتئین، دینامیک گیرندههای غشایی و طراحی دارو استفاده میشود.
CHARMM (Chemistry at HARvard Macromolecular Mechanics): این فورسفیلد، که رقیب دیرینه و سرسخت AMBER محسوب میشود، برای بیومولکولها طراحی شده است. توسعهی آن در دانشگاه هاروارد، منجر به ایجاد یک اکوسیستم غنی از نرمافزارها و ابزارها شده است. CHARMM طیف گسترده و بسیار مفصلی از پارامترها را نه تنها برای ماکرومولکولهای استاندارد، بلکه برای لیپیدهای غشایی، یونها و مولکولهای کوچک مختلف ارائه میدهد.
GROMOS (GROningen MOlecular Simulation): فورسفیلد GROMOS با یک انتخاب طراحی جالب توجه و جسورانه، راهکاری برای افزایش سرعت ارائه میدهد: «مدل United-Atom». در این مدل، اتمهای هیدروژن غیرقطبی (مثل هیدروژنهای متصل به کربن در یک زنجیره آلکان) به اتم کربن متصلشان "چسبانده" میشوند و به عنوان یک ذرهی واحد مدل میشوند. این کار به طور موثر تعداد ذرات سیستم را کاهش داده و بار محاسباتی را به میزان قابل توجهی کم میکند، در حالی که دقت قابل قبولی برای بسیاری از کاربردها حفظ میشود.
OPLS (Optimized Potentials for Liquid Simulations): همانطور که از نامش پیداست، فلسفهی اولیهی توسعه این فورسفیلد، شبیهسازی دقیق خواص مایعات بود. به همین دلیل، OPLS در پیشبینی خواص ترمودینامیکی مانند چگالی، آنتالپی تبخیر و به طور خاص، انرژیهای هیدراتهسازی (Solvation Energies)—که برای مطالعه برهمکنشهای پروتئین-لیگاند حیاتی است—بسیار دقیق عمل میکند. نسخههای مدرن آن (مانند OPLS-AA) برای بیومولکولها نیز به طور گسترده استفاده میشوند.
انتخاب یک فورسفیلد مناسب، یک تصمیم استراتژیک است. این انتخاب کاملاً وابسته به سیستم مورد مطالعه (آیا یک پروتئین است؟ یک پلیمر مصنوعی؟ یک سطح کانی؟)، پرسش علمی شما (آیا به دینامیک سریع علاقه دارید یا محاسبه انرژی آزاد اتصال؟) و در نهایت، سازگاری فورسفیلد با نرمافزار شبیهسازی شما دارد.
جمعبندی و چشمانداز به آینده: پس از نیرو، چه میآید؟
در این بخش، به عمق قلب تپندهی شبیهسازی دینامیک مولکولی سفر کردیم. دریافتیم که فورسفیلدها چگونه با یک سادهسازی، پیچیدگی غیرقابل تصور دنیای کوانتومی را در قالب معادلاتی کارآمد و قابل محاسبه درمیآورند و به ما این توانایی را میدهند که نیروی وارد بر هر اتم را در هر لحظه از زمان محاسبه کنیم.
با این حال، داستان شبیهسازی به همین جا ختم نمیشود. داشتن نیرو تنها نیمی از راه است. یک قطعهی نهایی و به همان اندازه حیاتی از پازل باقی مانده است:
حالا که نیروها را داریم، چگونه این نیروها را به حرکت تبدیل کنیم؟ چگونه معادلات دیفرانسیل پیچیدهی حرکت نیوتن را برای یک سیستم چندذرّهای حل کرده و مسیر تکامل سیستم را در زمان پیشبینی کنیم؟
پاسخ این پرسش، در دنیای زیبا و پر از چالش الگوریتمهای انتگرالگیری (Integration Algorithms) نهفته است.
در قسمت 3 این مجموعه، به این دنیا قدم خواهیم گذاشت. با روشهای معروف و پرکاربردی مانند الگوریتم ورله (Verlet) و Leap-frog آشنا خواهیم شد و خواهیم فهمید که این الگوریتمها چگونه با گامهای زمانی فوقالعاده کوچک (فمتوثانیه)، هستهی محاسباتی و موتور پیشران هر شبیهسازی دینامیک مولکولی را تشکیل میدهند. با هم بررسی خواهیم کرد که چگونه این روشها، پایداری عددی شبیهسازی را حفظ کرده و انرژی کل سیستم را کنترل میکنند.
پیشنهاد ویژه
در مرکز پژوهشهای رایانهای ایلیا ما تلاش میکنیم با ارائهی آموزشهای تخصصی، شبیهسازیهای علمی و تحلیل دادهها در زمینهی نرمافزارهای محاسبات مولکولی، به پژوهشگران کمک کنیم تا درک عمیقتر و دقیقتری از دینامیک سیستمهای مولکولی بهدست آورند.
آموزش مقدماتی مبانی شبیه سازی دینامیک مولکولی
